Akustiske størrelser, del 1: Hva er desibel?

Vi har tidligere skrevet her om hva lufttrykk er. Lyd er, kort sagt, raske svingninger i dette lufttrykket – lufta blir litt tettere, så litt tynnere, tettere, tynnere, og så videre. Trykksvingningene starter ved lydkilder, for eksempel høyttalere, og brer seg ut som bølger. Ved en «bølgetopp» har lydbølgen fortettet lufta på sitt meste, og ved en «bølgebunn» har lydbølgen fortynnet lufta på sitt meste.

Når disse lydbølgene treffer ørene våre, blir de oversatt av hørselssystemet vårt til noe som vi kan oppfatte bevisst – vi hører at lyden er der. Det er likevel vanskelig å beskrive, sammenligne og behandle slike subjektive opplevelser. For eksempel, vil du og jeg være enige om at den lyden er kraftigere enn den lyden? Og i så fall, hvor mye kraftigere?

For å gjøre lyd til noe som vi kan måle, beskrive, sammenligne og behandle, har det blitt innført mange forskjellige akustiske målestørrelser. Disse brukes til å gjøre lyd til noe vi kan snakke om mer konkret og objektivt. De påvirker oss alle, ikke minst fordi de brukes i støyreguleringer som bestemmer hvor mye lyd for eksempel flyplasser, veier og konserter har lov å lage. I denne artikkelserien skal vi derfor gå gjennom de viktigste akustiske størrelsene. I denne delen begynner vi med å diskutere hva desibel (eller decibel, på engelsk) er. Dette er en grunnleggende målestørrelse som vi finner igjen overalt der det snakkes om lyd.

Hvordan oppfatter vi lydstyrke?

I utgangspunktet måler vi lydtrykk som avviket fra det tilnærmet konstante atmosfæretrykket, som du kan se i figuren nedenfor. (Siden lydtrykket også er et trykk, måler vi det følgelig også i trykkenheten Pascal.) Når lydbølgene blir kraftigere, altså når forskjellen i trykk mellom bølgetopp (fortetting av lufta, med positivt lydtrykk) og bølgebunn (fortynning av lufta, med negativt lydtrykk) blir større, oppfatter vi selvfølgelig også at lyden blir kraftigere. Men måten vi oppfatter det på er ikke helt opplagt. La oss undersøke det nærmere.

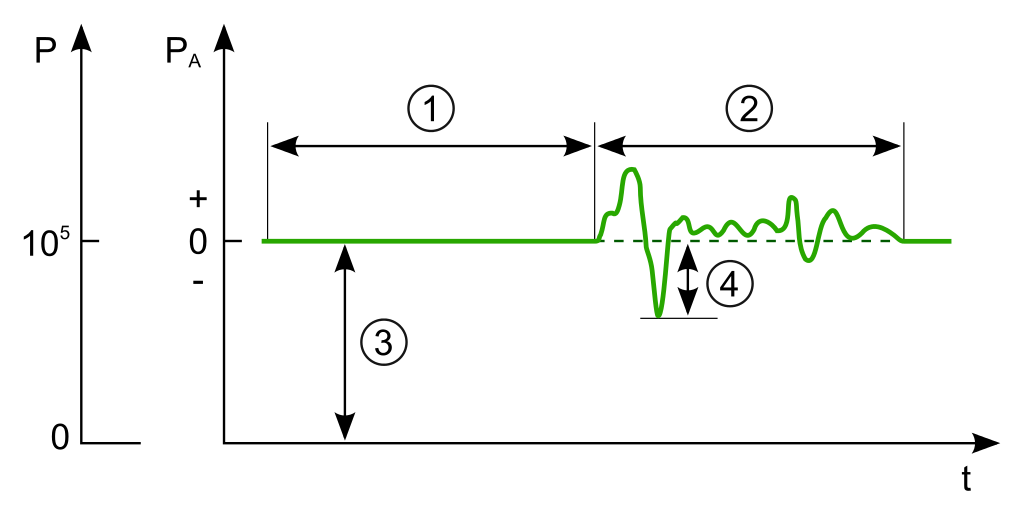1. Stillhet. 2. Hørbar lyd. 3. Atmosfæretrykk (ca. 100 000 Pascal). 4. Lydtrykk. [Bilde: Wikipedia-brukeren CLI]

La oss si at vi tar en lyd og dobler lydtrykket. Dette oppfatter vi som en markant økning. Deretter tar vi den originale lyden og tredobler lydtrykket. Hvis vi hører på disse tre lydene, vil de fleste høre at økningen fra dobbelt lydtrykk til tredobbelt lydtrykk oppfattes svakere enn økningen fra originalt til dobbelt lydtrykk.

La oss i stedet si at vi tar det doblede lydtrykket og dobler det igjen, slik at vi får et firedobbelt lydtrykk sammenlignet med det originale lydtrykket. Hvis vi sammenligner disse tre lydene, vil vi høre at økningen fra dobbelt til firedobbelt lydtrykk oppfattes like kraftig som økningen fra originalt til dobbelt lydtrykk. Med andre ord, hvis vi øker lyden med en gitt faktor (for eksempel 2, som i dette eksempelet med dobling) vil de fleste oppfatte økningen som omtrent like sterk, uavhengig av hvor kraftig lyden originalt var!

Du kan prøve ut dette selv her:

Lydtrykk	Lyd
Originalt
Dobbelt
Tredobbelt
Firedobbelt

Lydtrykknivå og desibel

Typiske lydtrykk og lydnivå. [Bilde: Occupational Safety and Health Administration, USA]

Siden hørselen vår fungerer som den altså gjør, gir det mening å bruke en logaritmisk enhet for å beskrive lydstyrke. (Vi kommer snart tilbake til hvorfor!) Lydtrykk-nivå er derfor definert som

$L_p = 20 \times \log \left( \frac{p_\text{rms}}{p_\text{ref}} \right) \, .$

Her er $L_p$ lydtrykknivået i desibel (som vanligvis forkortes til dB), $p_\text{rms}$ er et representativt lydtrykk for lyden vi skal regne ut lydnivået til og $p_\text{ref}$ er et referansetrykk på 0.00002 Pascal (altså 20 mikro-Pascal). Når vi angir lydstyrke i desibel, vil det altså egentlig bare si at vi uttrykker det fysiske lydtrykket på denne logaritmiske formen.

Så, hvorfor bruker vi egentlig en logaritmisk form som dette? Ut fra diskusjonen over, vet vi at hvis vi for eksempel dobler lydtrykket fra 0.5 Pascal til 1 Pascal, og deretter dobler det igjen til 2 Pascal, vil begge økningene oppfattes som omtrent like kraftige. Men hva blir lydtrykknivået i desibel? Hvis vi putter inn disse tallene i formelen over, finner vi ut at de tre lydtrykknivåene blir 88 dB, 94 dB, og 100 dB – lydtrykknivået øker altså med 6 dB hver gang lydtrykket dobles. (Tilsvarende kan vi finne ut at tidobling av lydtrykket gjør at lydnivået øker med 20 dB.)

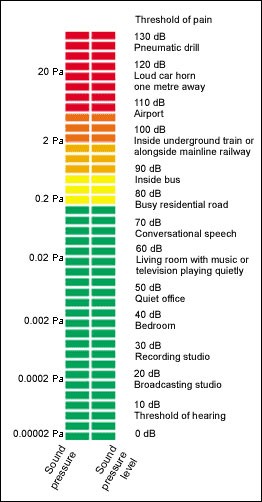
Dette er altså et poeng med å bruke desibel – hvis man legger til så-og-så-mange desibel til et lydtrykknivå, oppfattes økningen som like kraftig uavhengig av hva det originale lydtrykknivået var. Et annet poeng med desibel er at menneskelig hørsel strekker seg over et så stort spenn av lydtrykk: Den svakeste lyden unge mennesker med «normal hørsel» kan høre er på omtrent 0.00002 Pascal, og lyden fra et trykkluftbor – der man må bruke hørselvern for å ikke bli hørselsskadet – kan ligge rundt 60 Pascal. Da er det lettere å si i stedet at disse lydene er på 0 dB og på 130 dB.

(Desibel brukes forøvrig ikke bare for lydtrykk – det som egentlig kjennetegner desibel er at det er forholdstall som regnes ut fra logaritmiske formler som den over. Når man bruker desibel for andre ting innenfor f.eks. akustikk, elektronikk og signalbehandling, bytter man ut lydtrykket og referansetrykket med en annen målestørrelse og en annen referansestørrelse.)

Representativt lydtrykk: RMS

Som vi nettopp så, brukes et representativt lydtrykk $p_\text{rms}$ for å regne ut lydtrykknivået i desibel. Som vi ser fra figuren over, er lydtrykket egentlig noe som varierer raskt over tid, mens det representative lydtrykket er ett enkelt tall. Men hvordan regnes dette tallet ut?

Det representative lydtrykket går også under et annet navn: Root-mean-square, som på norsk blir kvadratrot-gjennomsnitt-kvadrat, og som vanligvis forkortes til RMS. Utregninga ligger egentlig litt i navnet – hvis vi representerer trykket ved tidspunktet $t$ som $p(t)$ , tar vi først kvadratet av trykket, altså $p^2(t)$ , tar deretter gjennomsnittet av det over en passende tidsperiode $T$ , og så til slutt tar vi kvadratroten av dette. For den som vil ha det helt konkret, uttrykkes dette matematisk som

$p_\text{rms} = \sqrt{ \frac{1}{T} \int_{t_0}^{t_0+T} p^2(t) \, \text{d}t } \, ,$

hvor vi velger å ta gjennomsnittet fra et tidspunkt $t_0$ til tidspunktet $t_0+T$ .

Å regne ut et representativt lydtrykk på denne måten gir riktignok bare mening for jevne lyder, som jevn tett trafikk eller ventilasjonssus, der $p_\text{rms}$ er ganske uavhengig av lengden av perioden vi tar gjennomsnittet over. For korte, skarpe lyder som et klapp eller en eksplosjon, derimot, blir $p_\text{rms}$ mindre jo lengre tidsperioden er, siden en større andel av tidsperioden da blir stillhet. Hvordan vi finner et godt representativt lydtrykknivå for slike lyder kommer vi tilbake til seinere i denne artikkelserien.

Hva blir lydtrykknivået når vi har flere lyder samtidig?

To biler lager høyere lydtrykk enn én bil, men *ikke dobbelt så høyt*. [Bilde: Greg Gjerdingen]

Til slutt skal vi se litt på hvordan lydtrykknivået øker når vi har flere lyder samtidig. Hvis vi har to lyder samtidig, for eksempel to biler som går på tomgang ved siden av hverandre, er det fristende, men feil, å tro at lydtrykknivået blir

$20 \times \log \left( \frac{p_\mathrm{rms,1}+p_\mathrm{rms,2}}{p_\mathrm{ref}} \right) \, ,$

hvor $p_\mathrm{rms,1}$ og $p_\mathrm{rms,2}$ er RMS-lydtrykket fra henholdsvis bil 1 og bil 2.

Grunnen til at dette blir feil, er at lydbølgene fra de to bilene ikke er akkurat de samme. I lydbølgen fra den ene bilen vil ikke bølgetoppene og bølgebunnene komme akkurat samtidig som de i lydbølgen fra den andre bilen, og vi får derfor ikke ren konstruktiv interferens. I stedet interfererer de to lydbølgene både litt konstruktivt og litt destruktivt, slik at det totale RMS-lydtrykket blir $p_\mathrm{rms} = \sqrt{p^2_\mathrm{rms,1}+p^2_\mathrm{rms,2}} \, .$ Dette er mer enn RMS-lydtrykket fra én bil, men mindre enn summen av RMS-lydtrykkene fra hver av bilene.

Dermed blir det totale lydtrykknivået fra disse to lydkildene

$L_p= 20 \times \log \left( \frac{\sqrt{p^2_\mathrm{rms,1}+p^2_\mathrm{rms,2}}}{p_\mathrm{ref}} \right) = 10 \times \log \left( \frac{p^2_\mathrm{rms,1}+p^2_\mathrm{rms,2}}{p^2_\mathrm{ref}} \right) \, .$

(Her har vi to likeverdige formler for lydtrykknivået; den første følger av det vi har sett tidligere, mens den siste er mer praktisk å trykke inn på kalkulatoren. De to formlene er likeverdige fordi $20 \times \log (x) = 10 \times \log (x^2)$ .)

Hvis de to bilene lager akkurat like mye lyd (altså hvis $p_\mathrm{rms,1}=p_\mathrm{rms,2}$ ), kan vi regne ut at de lager 3 dB mer lyd enn én bil gjør alene. Dette gjelder også for trafikk: Hvis trafikken på en veistrekning for eksempel dobles fra 2000 bilpasseringer per time til 4000 bilpasseringer per time, øker det totale lydnivået med 3 dB – en merkbar økning, men langt mindre kraftig enn man kanskje skulle tro.

Neste gang

Enda har vi bare begynt å se på akustiske størrelser – de størrelsene som brukes i støyreguleringer i Norge og internasjonalt er mer avanserte, og krever mer forklaring. Neste gang skal vi se på frekvensveiing, altså hvordan vi kan ta hensyn til at menneskeører ikke hører alle lyder like godt, selv om lydenes RMS-lydtrykk er like.

Gå til Akustiske størrelser, del 2: Frekvensveiing…

Facebook

Twitter