Så langt i denne serien har vi sett på hva lydtrykknivå og desibel er, og hvordan vi kan regne ut lydtrykknivå på en måte som tar hensyn til hvordan vi mennesker hører. Enda har vi bare diskutert lyder som er helt jevne og ikke forandrer seg, slik som ventilasjonsstøy og maskiner som står og går jevnt. Men hva med lyder som forandrer seg, som forbipasserende biler eller fly, eller eksplosjoner og andre smell? Heldigvis har det blitt innført akustiske størrelser og teknikker som gjør at vi kan beskrive og sammenligne også slike lyder, blant annet Slow- og Fast-veiing, lydeksponeringsnivå og ekvivalentnivå. Det er disse vi skal ta for oss i denne delen.
Veiing, Fast og Slow
I første del så vi hvordan vi kan regne ut et lydtrykknivå fra et representativt trykk, nemlig RMS-trykket. For å finne RMS-trykket tar vi en måling av lydtrykket til en jevn lyd over en lang nok stund, og koker det ned til ett representativt tall for den lyden. Men hvis vi skal finne lydtrykknivå for en lyd som varierer betydelig, kan vi i stedet finne et lydtrykknivå som varierer med tid: Hvor sterk er lyden nå? Hvor sterk var den for ett sekund siden? Eller ett minutt siden?
Derfor har det blitt innført forskjellige måter å veie i tid på. Disse tidsvarierende lydnivåene er kun basert på lyden i løpet av det siste øyeblikket. Det brukes noen forskjellige slike tidsveiinger. De to mest brukte har de herlig enkle og beskrivende navnene Slow og Fast og er bygd opp likt.
Eksponensiell tidsveiing
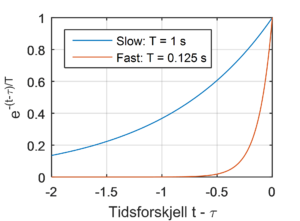
Mer konkret, skjer denne tidsveiinga gjennom de eksponensielle funksjonene som du kan se i figuren til høyre. Disse synker mot null jo lenger bak vi går i tid. Det som skiller Slow og Fast er hvor fort denne tidsveiinga synker. Fast har en «tidskonstant» på 0,125 sekunder, og som du kan se i figuren, vil det si at den så godt som ikke tar hensyn til det som skjedde for mer enn et halvt sekund siden. Slow har en åtte ganger lenger tidskonstant på 1 sekund, som vil se at den «ser» åtte ganger lenger tilbake i tid.
Så, hvordan bruker vi disse tidsveiingsfunksjonene? På samme måte som når vi regner ut RMS-trykket, tar vi utgangspunkt i kvadratet av lydtrykket, Nå bruker vi imidlertid en tidsveiingsfunksjon på det kvadrerte lydtrykket i stedet for å regne ut et rent gjennomsnitt. Helt konkret, uttrykkes dette matematisk som
hvor er tidspunktet vi ønsker å regne ut lydtrykknivået for, og
er tidskonstanten til Slow eller Fast. Ut fra hvilken vi velger, får vi enten Slow-veid lydtrykk
eller Fast-veid lydtrykk
. Disse kan i sin tur brukes til å regne ut Slow- eller Fast-veid lydtrykknivå,
På klokelig vis er formlene for Slow- og Fast-veid lydtrykk designet slik de gir lydtrykknivå som tilsvarer den enklere RMS-framgangsmåten for helt jevne lyder.
Eksempler
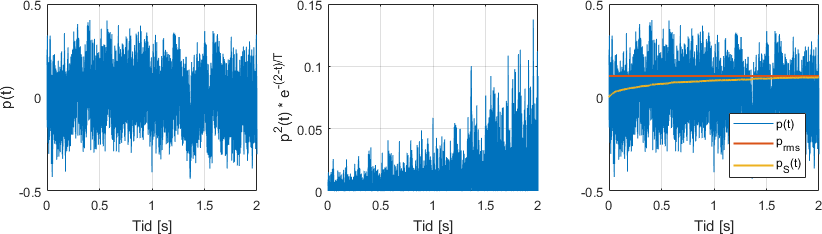
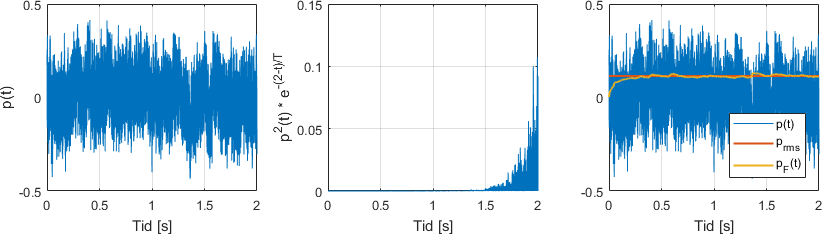
La oss se på eksemplene av Slow- og Fast-veiing nedenfor, for å gjøre det helt klart. I begge eksemplene bruker vi et to sekunders støt av jevn rosa støy som starter ved . (Vi antar at det er helt stilt før da.) Denne støyen kan du se i underfigurene til venstre. Underfigurene i midten viser hvordan vi vekter det kvadrerte lydtrykket når vi skal regne ut henholdsvis Slow og Fast-veid lydtrykk for
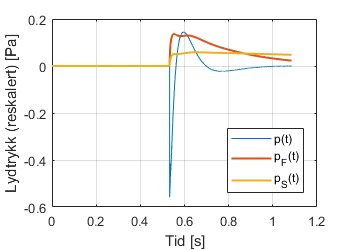
Underfigurene til høyre sammenligner de tidsvarierende Slow- og Fast-lydtrykkene
og
med RMS-lydtrykket
I begge tilfellene ser vi at Slow- og Fast-veid lydtrykk til slutt tilsvarer RMS-lydtrykket. Siden Fast ser kortere tilbake og dermed reagerer raskere, går den fortere mot RMS-lydtrykket. Samtidig ser vi at Fast svinger litt mer opp og ned. Siden den ser kortere tilbake, er den mer påvirket av kortvarige tilfeldige forandringer i støyen – ingen støy er perfekt jevn!
Slow
Fast
Merk at i disse eksemplene er det Slow- og Fast-veid lydtrykk i Pascal vi viser, og ikke lydtrykknivået i desibel. For å finne lydtrykknivået fra lydtrykket, må vi bruke formelen ovenfor.
Oppsummering
Både Slow og Fast tidsveiing gir lydtrykknivå ut fra det som har skjedd det siste øyeblikket, men de har litt forskjellige bruksformål:
- Slow-veide lydtrykknivå
ser lenger tilbake i tid, som gjør at nivået blir jevnere i tid ved å undertrykke skarpe lyder og tilfeldige variasjoner i lyden. Slow er best for å måle på lyder som varierer sakte, som lyden fra forbipasserende fly.
- Fast-veide lydtrykknivå
ser kortere tilbake i tid, som gjør at nivået blir ujevnere, men som også gjør at skarpe lyder blir fanget opp. Fast er best for å måle på kortere lyder, for eksempel smell og eksplosjoner. Se for eksempel hvor mye mer Fast reagerer enn Slow på figuren til høyre.
- For jevne lyder der styrken ikke varierer med tid, vil Slow og Fast begge tilsvare RMS-basert lydtrykknivå.
Maksimalnivå
Slow og Fast tidsveiing fungerer fint når vi skal se på hvordan lydnivået varierer med tid. Tidsvarierende akustiske størrelser er imidlertid vanskelig å karakterisere støyhendelser med, for eksempel eksplosjoner eller passerende fly. Vil vi heller ha ett tall som beskriver hvor kraftig lyden er.
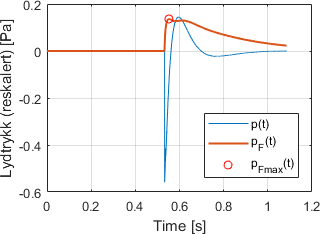
Den enkleste måten å finne et slik tall på, er å simpelthen hente ut den høyeste verdien i kurver for Slow- eller Fast-veid lydtrykk eller lydtrykknivå. Det gir oss en pekepinn på hvor kraftig lyden er på sitt sterkeste. For eksempel, i figuren til høyre ser vi hvordan vi finner Fast-veid maksimallydtrykk. Maksimallydtrykknivået regnes da ut fra dette som
Hvis vi allerede har kurver for Slow- eller Fast-veid lydtrykknivå, kan vi også finne maksimalnivået rett fra disse. Resultatet blir det samme.
Støydose: Lydeksponeringsnivå

En svakhet med maksimalnivå er at det bare sier noe om hvor kraftig lyden er på sitt sterkeste. Det sier ingenting om hvor lenge lyden varer. For eksempel, kan vi få samme maksimalnivå fra et helikopter som flyr over deg og et helikopter som svever over deg i en time, selv om den sistnevnte hendelsen naturligvis er langt mer plagsom.
Som et alternativ har vi lydeksponeringsnivået (som på engelsk heter sound exposure level, eller SEL). Det gir oss et tall på hvor mye lyd vi har blitt eksponert for alt i alt over en tidsperiode. Dermed blir det altså en slags støydose. Denne tidsperioden kan være lang, f.eks. en konsert eller en arbeidsdag, eller den kan være kort, f.eks. en enkelt støyhendelse som en flypassering.
Lydeksponeringstrykket regnes ut nesten på samme måte som RMS-trykket, som vi forklarte i første del av denne serien, med én forskjell. Når vi regner ut RMS-trykket, integrerer vi kvadratet av lydtrykket over et tidsintervall og deler på lengden av tidsintervallet for å få gjennomsnittet av det kvadrerte lydtrykket. Når vi regner ut lydeksponeringstrykket, deler vi i stedet på en referansetid på ett sekund:
Deretter regner vi ut et lydeksponeringsnivå fra dette lydeksponeringstrykket:
Eksempel
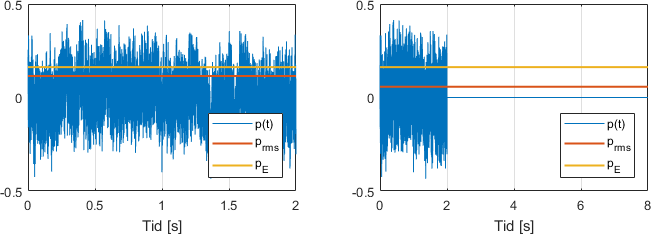
La oss se på lydeksponeringstrykket og RMS-lydtrykket for to tilfeller. I det første tilfellet, har vi et to sekunder langt klipp av rosa støy. I det andre, har vi det samme klippet, etterfulgt av seks sekunder med stillhet. La oss sammenligne de to tilfellene i figurene nedenfor. Vi kan se at RMS-lydtrykket er lavere i det andre tilfellet, mens lydeksponeringstrykket er det samme i begge tilfellene. Grunnen til at RMS-lydtrykket minker, er at den påfølgende stillheten gjør at lyden gjennomsnittlig sett er svakere. Lydeksponeringstrykket regnes derimot ut fra bare hvor mye lyd det var totalt i måleperioden, og er derfor likt i begge tilfeller.
Hva forteller lydeksponeringsnivået oss? Det er jo litt abstrakt, og det er vanskelig å sammenligne det direkte med det vanlige RMS-lydtrykknivået. Vi kan likevel fint sammenligne forskjellige lydeksponeringsnivå med hverandre. For eksempel, ta to arbeidere som går med støydosimeter gjennom sin arbeidsdag. Vi kan da i etterkant sammenligne begges lydeksponeringsnivå for å se hvem som har blitt eksponert for mest støy.
Ekvivalentnivå
Som lydeksponeringsnivået, ligner ekvivalentnivået ligner på RMS-lydtrykknivå. Den eneste forskjellen mellom dette og lydeksponeringsnivået er at i stedet for å samle all støyeksponeringen på ett sekund, sprer ekvivalentnivået støyeksponeringen over en lengre periode ved å regne ut et ekvivalenttrykk og ekvivalentnivå som
Ekvivalentnivået tar da støyeksponeringen fra en tidsperiode og sprer den over den samme (eller en annen) tidsperiode.

For eksempel kan vi ta all støyen du har blitt eksponert for i løpet av i går, og spre den utover 24 timer. Dette gir oss 24-timers ekvivalentnivået , men hva forteller det oss? Jo, dette ekvivalentnivået tilsvarer lydtrykknivået til en jevn lyd som gir den samme støydosen som all den lyden ekvivalentnivået er basert på.
Hvis ekvivalentnivået er basert kun på én støyhendelse blir det en litt abstrakt støymål på samme måte som lydeksponeringsnivået. Hvis vi derimot regner ut f.eks. et entimers ekvivalentnivå for rushtidstrafikk, blir dette ekvivalentnivået en fin og representativ størrelse for det tidsvarierende lydtrykknivået i den perioden. Derfor er norske støyreguleringer hovedsaklig basert rundt spesielle varianter av ekvivalentnivå, som vi kommer tilbake til i neste del.
Kombinasjon med frekvensveiing
Hvordan henger denne tidsveiinga sammen med frekvensveiing? Det er ikke vanskelig å kombinere de to. Som vi beskrev i forrige del, gjøres frekvensveiinga ved at vi filtrerer det originale lydtrykket for å få f.eks. et A-veid lydtrykk
. Dette frekvensveide lydtrykket kan i sin tur tidsveies for å få f.eks. et A-frekvensveid og Fast-tidsveid lydtrykknivå
eller et A-frekvensveid lydeksponeringsnivå
. I praksis innebærer nesten alle offentlige støyreguleringer en kombinasjon av A-frekvensveiing og en eller annen tidsveiing.
Neste gang
I disse tre delene har vi forklart de forskjellige byggesteinene i de akustiske størrelsene som brukes i offentlige reguleringer. Disse reguleringene bruker imidlertid mer avanserte størrelser som gir et bedre bilde av hvor plagsom en støysituasjon er. (Vi har tidligere skrevet om koblingen mellom støy og støyplage.) I neste del skal vi gå gjennom de mer avanserte størrelsene som brukes i norske støyreguleringer.